Rydberg & Bohr

[Kristen Kim 2K]

Can someone explain the relationship between Rydberg's equation and Bohr frequency condition?

[AustinGrove3B]

Ep = E2 - E1

where Ep is the energy of the photon, E2 is the energy of the excited electron, and E1 is the energy of the electron before excitation. In concert with our knowledge of E=hv, we can mathematically iterate this phenomenon known as Bohr's Frequency Condition that solves for the frequency of incident light:

hv = (E1 - E2)
v = (E1 - E2)/h

Note that it was experimentally determined that the energy En at a given energy level is equal to -hR/n^2, where h is Planck's constant and R is the Rydberg constant (3.29*10^15 s^-1). The convention is that an electron with no relation to the atom would be at an infinitely high energy level n and thus its energy would approximate 0. Therefore, electrons in orbit are said to have negative energy since their energy is lower than that of a freed electron. Thus we can extend upon Bohr's Frequency condition as follows:

v= (-hR/(n1)^2 - -hR/(n2)^2)/h [replace E with -hR/n^2]
v= -hR(1/(n1)^2 - 1/(n2)^2)/h [factor out -hR]
v=-R(1/(n1)^2 - 1/(n2)^2) [h cancels, we are left with the Rydberg eqn]

[Andonios Karas 4H]

The Bohr Frequency Condition, 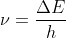, states that the frequency is directly related to the energy of photons emitted as electrons move down energy levels. The higher the frequency, the greater the energy in each photon.

Rydberg's Equation, E_n =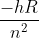 , is used to calculate the energy of an electron in different energy levels of a Hydrogen atom.

We can use these equations in conjunction in order to understand the energy of photons emitted as an electron moves from higher energy level to a lower energy level in an atom.

Using the Rydberg Equation, we can calculate the energy of the electron in the initial and final energy level, and find the difference to give the energy of the photon or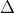 E.

Using the Bohr Frequency Condition and the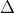 E from the previous calculation, we can solve for the frequency of light emitted.